‘힘’과 물리적 법칙

정형식 교사의 수학 과학 비타민

정형식 교사의 과학 비타민 /

무엇인가를 이해하려 할 때, 실물을 보지 않으면 실감이 나지 않는다. 코끼리라는 것이 도대체 무엇일까를 여러 번 묻기보다 실제 코끼리를 보는 것이 코끼리에 대해 더 잘 알 수 있다. 그러나 세상에는 눈에 너무나 잘 보이기 때문에 오히려 보이지 않는 것들도 있다. 흔히들 “물리를 공부해도 물리를 모른다”는 말을 한다. 내 입장에서도 ‘물리를 공부하고 물리를 가르쳐도 물리를 정말 알까?’하고 내 자신에게 묻곤 하면 그 답에 대해 확신이 서지 않는다. 어떤 일에 푹 젖어 있다 보면 너무나 당연하게 알아야 할 것도 놓쳐버리게 되는 경우가 있다. 숲 속으로 깊이 들어가면 나무는 보이지만 숲이 보이지 않는 것이다.

물리에서 ‘힘’이라는 것도 그런 것이라고 생각된다. 물리에서 ‘힘’은 너무나도 자주 등장하는 중요한 개념이지만, 너무나 당연하게 알아야 할 것을 놓치는 수가 있다. 고등학교 물리1 교육과정에서 ‘I. 힘과 에너지’단원에서 등장하는 힘에 대한 내용들을 살펴봄으로써 힘에 대한 이해를 높여보도록 하자. ‘I. 힘과 에너지’단원에서 등장하는 소단원들은 다음과 같다.

(1) 속도와 가속도 (2) 운동의 법칙 (3) 운동량과 충격량 (4) 일과 에너지

이 단원들은 서로 유기적인 관계가 있기 때문에 과학적 사고력을 향상시키기 위한 글쓰기로서 좋은 재료가 될 수 있다. 특히 각 소단원을 서로 연결시켜주는 물리량으로 여러 가지를 생각할 수 있겠지만 빼놓을 수 없는 중요한 것 중의 하나가 바로 힘이다.

여기서 다음의 간단한 문제를 풀어보자.

( ㉠ ) = 힘 × ( ㉡ )

위의 식에서 ㉠과 ㉡에 들어갈 물리량은 무엇이 있을까? 물론 답은 여러 개가 가능하므로 할 수 있는 한 많은 예들을 찾아보도록 하자. 아는 만큼 찾을 수 있을 테니까.

특별한 기준없이 무작위로 가능한 예를 찾는 것보다는 물리 교과서의 각 단원들을 살펴보면서 가능한 예를 찾는 것이 바람직하다.

우선 (1) 속도와 가속도 단원에서는 힘이 특별히 등장하지는 않기 때문에 위의 식과 관련된 내용은 거의 없다.

(2) 운동의 법칙 단원에서는 일단 뉴턴의 운동 제 2 법칙을 고려하면 F=ma 라는 식이 등장한다. 이 식으로부터 가능한 형태로는 ㉠ 가속도 ㉡ 1/질량 이 있다.

(3) 운동량과 충격량 단원에서는 충격량의 정의를 생각할 때 I=F·t 라는 식이 있으므로 이로부터 가능한 형태로는 ㉠ 충격량 ㉡ 시간 이 있다.

(4) 일과 에너지 단원에서는 일의 정의인 W=F·s 와 양변을 시간으로 나눌 때 등장하는 일률을 고려하면 P=F·v를 생각할 수 있으므로 가능한 형태로는 ㉠ 일 ㉡ 이동 거리 또는 ㉠ 일률 ㉡ 속도 등이 가능하다.

이 밖에도 또 다른 형태로 가능한 것이 있다. 각자가 한번 생각해 보도록 하자.

이제 힘에 대해 어느 정도 준비 운동이 되었다고 생각하고, 교과서를 활용한 다음 문제를 풀어보도록 하자.

[논제] 야구 경기에서 투수가 던진 빠른 공을 포수가 받는다. 포수가 공을 잡기 시작하여 공이 멈출 때까지 포수가 공에 힘을 가한 것을 그래프로 나타낼 때, 그래프 (가)는 시간에 따라 포수가 공에 힘을 가한 것을 나타낸 것이고, 그래프 (나)는 거리에 따라 포수가 공에 힘을 가한 것을 나타낸 것이다.

두 개의 그래프에서 그래프 아랫부분의 넓이는 어떤 물리량을 나타내는지 설명하고, 만약 투수가 공을 2배의 속력으로 던진다면 (가)와 (나)의 그래프에서 그래프 아랫부분의 넓이가 어떻게 변하게 될지 설명하여라.

과학에서는 그래프가 중요한 경우가 많다. 그래프를 대할 때에는 그래프에서 나타나는 면적의 의미와 기울기의 의미를 항상 생각해보는 태도를 가지는 것이 중요하다. 일반적으로 그래프에서 기울기는 변화율 즉(y축 물리량) / (x축 물리량) 을 의미하고 면적은 (x축 물리량)×(y축 물리량)을 의미한다. 그래프 (가)에서 기울기는 (힘) / (시간) 이므로 특별한 물리량의 의미한다고 보기 어렵고, 면적은 (힘)×(시간)이므로 충격량 또는 운동량의 변화량을 의미한다. 그래프 (나)에서 기울기는 (힘) / (이동거리) 이므로 특별한 물리량의 의미한다고 보기 어렵고, 면적은 (힘)×(이동 거리)이므로 일 또는 운동 에너지의 변화량을 의미한다.

여기에서 투수가 공을 2배의 속력으로 던지게 되면 공의 운동량은 2배가 되고(P=mv) 이에 따라 공을 멈추게 하기 위해 포수가 공에 가해주어야 할 충격량도 2배가 되므로 그래프 (가)에서 그래프 아랫부분의 넓이는 2배가 된다. 그런데 운동 에너지를 고려할 때에는 공의 속력이 2배가 되면 공의 운동 에너지는 4배가 되므로

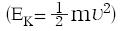공을 멈추게 하기 위해 포수가 공에 해주어야 할 일은 4배가 된다. 따라서 그래프 (나)에서 그래프 아랫부분의 넓이는 4배가 되어야 한다.

정형식/서울숭실고등학교 물리교사